1. 设b是正自然数,b进制数的一般形式是怎样的?

2. 用10100表示的数在二进制、八进制和十六进制下的数值分别是多少(用十进制数表示)?

3. 将下列数转化为十进制数:
(1)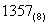 ;(2) ;(2)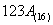 ;(3) ;(3)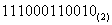

解答: (1)751;(2)4666;(3)3634。
4. 将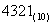 转化为二进制数、八进制数和十六进制数。 转化为二进制数、八进制数和十六进制数。

5. 尝试证明定理5、定理6、定理7。

6. 举实例说明半序集、全序集和良序集。

解答:当不规定花色的序时,52张牌按数字大小是半序集,当规定了花色的序后,52张牌先按数字大小,再按花色大小就是全序集,也是良序集。
7. 有血缘关系的家族内成员关于“辈分高低”关系构成全序集吗?亲戚成员关于“辈分高低”关系构成全序集吗?

8. 所有英文单词能构成全序集吗?

9. 用数学归纳法证明下列各题:
(1)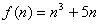 能被6整除; 能被6整除;
(2)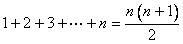 ; ;
(3)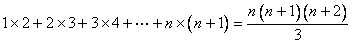 ; ;

解答:
用数学归纳法证明下列各题:
(1)(见“模块3练一练”)。
(2)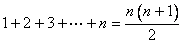 ; ;
i)当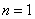 时,左=右=1,命题成立。 时,左=右=1,命题成立。
ii)设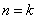 时, 时,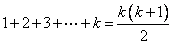
则当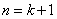 时, 时,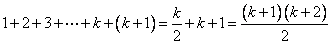 , ,
所以命题成立。
(3)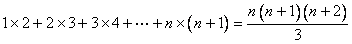 ; ;
i)当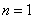 时,左 时,左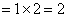 ,右 ,右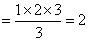 ,命题成立。 ,命题成立。
ii)设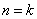 时, 时,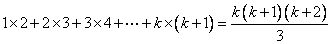 , ,
则当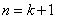 时, 时,
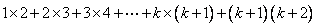 , ,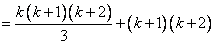
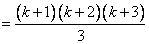
所以命题成立。
10. 已知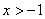 ,且 ,且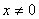 , ,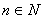 ,且 ,且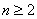 ,求证 ,求证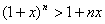

11. 已知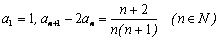 。 。
(1)猜想通项公式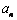 ; ;
(2)如何证明上述通项公式。

解答:(1)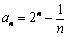 ; ;
(2)将通项公式代入递推公式,验证其是否成立。
12. 在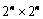 , ,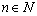 个相同的小方格组成的棋盘上,任意挖起一个小方格后,总可以用三个这样的小方格构成的L形图片恰好铺满。 个相同的小方格组成的棋盘上,任意挖起一个小方格后,总可以用三个这样的小方格构成的L形图片恰好铺满。

解答:i)当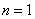 时, 时,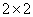 的方格如图所示: 的方格如图所示:
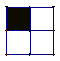
命题成立。
ii)当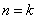 时,即 时,即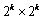 的方格时命题成立, 的方格时命题成立,
则当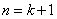 时,用四块 时,用四块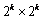 拼接如图所示: 拼接如图所示:

命题成立。
13. 证明可以把自然数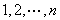 排成一圈,使每相邻两数之差不超过2。 排成一圈,使每相邻两数之差不超过2。

14. 两个小朋友做游戏:有数目相同的两堆火柴,每个小朋友间隔地在属于自己的那堆中取若干根火柴,每次至少取一根,规定取得最后一根火柴者为胜。求证后取者有必胜策略。

15. 已知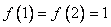 , ,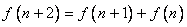 , ,
求证对任意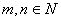 ,有 ,有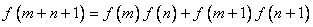 。 。

16. 已知对任意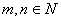 , ,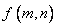 满足 满足
1)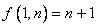 ; ;
2)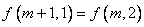 ; ;
3)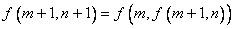 。 。
求证 1)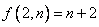 ; ;
2)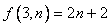 ; ;
3)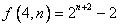 。 。

解答:(1)i)当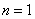 时, 时,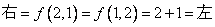 。 。
ii)设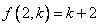 成立,则 成立,则
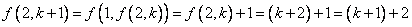 , ,
所以命题成立。
(2)i)当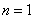 时, 时,
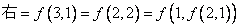
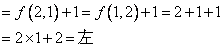 。 。
ii)设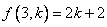 成立,则 成立,则
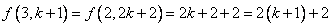 。 。
所以命题成立。
(3)i)当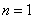 时, 时,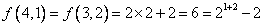 , ,
ii)设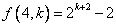 成立,则 成立,则
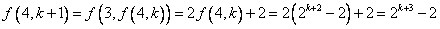 , ,
所以命题成立。
17. 说明:若自然数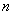 的标准分解式为 的标准分解式为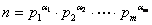 ,则 ,则
(1)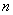 的一切正因数的个数为 的一切正因数的个数为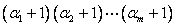 ; ;
(2)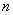 的一切正因数的和为 的一切正因数的和为
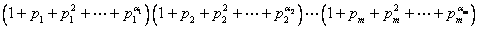 。 。

18. 证明形如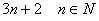 的素数有无限多个。 的素数有无限多个。

|



