学习目标：
了解数系拓展的原因、史料、人物和建构新数系的基本方法。
重点和难点：
重点了解数系的拓展过程；
难点对史料的解释。
数的发展历史 |
 |
数的概念产生于对实物的计量，通过物件的多少、长度、面积的度量，最终归结到数。事实上，真正从实体直接认识的数，只有自然数，其他的数都要经过程度不同的理性思考和抽象，才能被认识。
按照实践中与实物分离的程度不同，数的拓展途径如下：
自然数→正有理数→简单代数数（如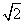
，
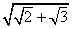等）→零和负有理数→虚数→复数。
今天我们研究数时，按照它的逻辑结构，一般呈现为如下的拓展过程：
自然数→整数→有理数→实数→复数。
可见，数概念拓展的真实历史发展与逻辑发展有很大的差异：人们在没有认识负数之前，就承认了有理数，并遇见了一些无理数。也就是说，人们在没有完整地认识整数之前，就开始进入到有理数集和实数集了。这和今天我们看到的数的逻辑结构很不一样。
为了叙述的方便，本课程在讲数的发展历史时，尽量兼顾到数的逻辑程序。
自然数 |
|
在人类漫长的生活和生产实践中，为了计量和辨别实物的多少，自然而然地产生了自然数。虽然自然数的概念已经与实物相脱离，具有一定的抽象性，但它终究与实体直接相关，可以由日常生活经验直接获得，即“自然”存在的数。而其他数都不具有这样“自然”的特征，都需要一些理性的处理才能被人们认识和接受。
（注意：原始的自然数概念不包含零，把零纳入自然数是最近的事情）
当人们对数的认识越来越明确时，感到有必要以某种方式来表达数，于是慢慢产生了计数方法和记数符号。最早产生的计数方法可能是手指计数，一只手上的5个指头可以被现成地用来表示不超过五个实物的集合，两只手上的指头可以表示不超过10个实物的集合。正如亚里士多德早就指出的那样，今天十进制被广泛采用，只不过是我们绝大多数人生来具有10个手指这样一个解剖学事实的结果。
当手指头不够用时，就出现了石子计数、结绳计数、刻痕计数等，以便表示更多实物的集合。例如用不同大小的石子表示不同的数：一颗小石子对应一个实物，一颗中石子对应5个（一只手）实物，一颗大石子对应10个（两只手）实物。在我国古代，曾经采用实物和结绳的办法计数：《周易·系辞下》记载“上古结绳而治，后世圣人，易之以书契”。东汉郑玄称：“事大，大结其绳；事小，小结其绳。结之多少，随物众寡”。例如小数字1、2、3等，用小实物 (如小木棍、小石子)表示，而10的整数倍则用结绳来表示，即在一根绳上打一个结表示10，打两个结表示20，打三个结表示30，象形汉字“十”、“廿”、“卅”就是结绳计数的证据之一。
又经历了漫长的发展，直到距今大约五千多年前，先后出现了用于书写的记数符号以及相应的概念。例如古埃及的象形数字、古巴比伦的楔形数字、中国甲骨文数字和筹算数字（汉字一、二、三就是筹算数字的演变）、希腊阿提卡数字、印度婆罗门数字和玛雅数字等等。其中除了巴比伦楔形数字采用六十进制、玛雅数字采用二十进制外，其他均属十进制数。好的数字符号使数的书写与运算更为便捷。
 |
 |
  |
结绳计数 |
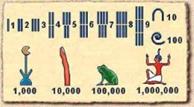
古埃及数字 |
古巴比伦的楔形数字、阿拉伯数字和中国筹算数字 |
罗马数字：（1）Ⅴ（5）Ⅹ（10）L（50）C（100）D（500）M（1000） XVIII, 18； XXXIV ，34；XCIX, 99
现在全世界流行的数码字（常称为阿拉伯数字）是印度人首创的，印度在数学家阿耶波多（公元476-550年）生活的年代已经用十进位制记数，但所用记号各地各时期不一样，零的记号也没有定型，经过漫长的改进，才成为比较完善的十进位制记数法。记载印度数学知识的各种译著经伊斯兰各国流传到欧洲，欧洲人就称其中的数码字为阿拉伯数字，直到19世纪，人们才发现，阿拉伯数字的发祥地是印度。
在生产和生活实践中，逐步产生了自然数的运算：由实物的收集和积累产生了加法和乘法，由实物的消耗和公平分配产生了减法和除法。在自然数的基础上，初等算术在几个古老的文明地区发展起来。
 |
 |
