无理数
在古代人在测量中，用一单位长的工具进行实物的测量，如果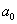
次量尽（
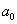是整数），那么该实物的长度就是一个正整数
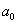；如果量不尽，那么用更小的度量工具，例如用
单位长量，如果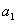
次量尽（
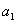是整数），那么该实物的长度就是
；如果还是量不尽，那么再用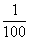
单位长量来量；……。当时的人们认为，这样一次次地缩小度量单位，总能够精确地量出实物的长度
（
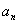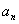为整数）。
早在公元前500年，希腊的毕达哥拉斯学派就提出“万物皆为数”，他们所说的数，事实上仅仅指整数和有理数（他们当时把分数看作两个整数之比）。但是该学派的成员希伯索斯发现，将两个边长为1的正方形裁拼成一个新的正方形（如图），新正方形的面积为2，而其边长c既不是整数，也不是整数的比所能表示。这就是说，现实世界中除了整数和分数之外，还有其他的数。
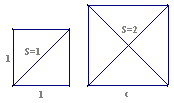
这个事实冲击了当时希腊数学家“万物皆为数”的传统见解，使他们深感不安，这个事件被称为历史上第一次数学危机。它对以后数学的发展产生了深远的影响，警示人们直觉和经验是不可靠的，从而推动了数学公理化的进程。15世纪意大利著名画家达.芬奇称这样的数为“无理的数”，导致我们今天就称它们为“无理数”。
无理数和有理数共同建立了对现实世界实物的数量及其运算的刻画，完善了毕达哥拉斯学派“万物皆为数”的观点。人们把无理数和有理数构成的数集称为实数集。
在实数集上，非负数的有理幂运算（
）是封闭的。
 |
 |
