
例16 已知在平面直角坐标系中,点 |
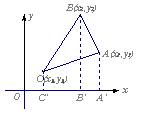
图7-7
解 设![]() 、
、![]() 、
、![]() 在
在![]() 轴上的投影分别是
轴上的投影分别是![]() 、
、![]() 、
、![]() ,因为三角形
,因为三角形![]() 的面积
的面积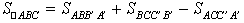 ,所以
,所以
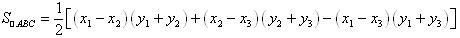
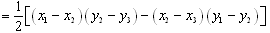
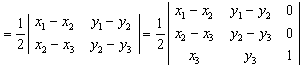
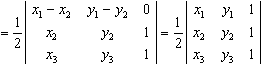 。
。
注根据行列式的性质,对换两行将改变行列式的符号,所以上述面积公式中三个顶点的排列顺序会改变计算结果的正负,但不会改变结果的绝对值。
上述三角形的面积公式等价于下列结论:
(1)以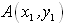 、
、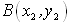 、
、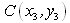 为顶点的平行四边形的面积等于
为顶点的平行四边形的面积等于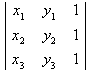 的绝对值。
的绝对值。
(2)平面上三点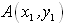 、
、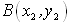 、
、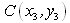 共线的充要条件是
共线的充要条件是
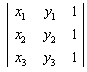 或
或 。
。
例17 设平面上三条两两相交的直线方程为
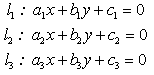 ,
,
求证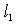 、
、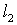 、
、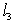 共点的充要条件是行列式
共点的充要条件是行列式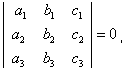 。
。
证明 因为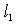 与
与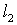 相交,所以方程组
相交,所以方程组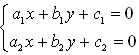 有唯一解,即
有唯一解,即![]() 与
与![]() 的交点坐标为
的交点坐标为
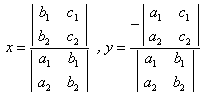 。
。
(必要性)因为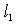 、
、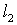 、
、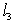 共点,所以
共点,所以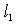 与
与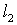 的交点在
的交点在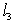 上,所以交点坐标满足
上,所以交点坐标满足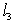 的方程,即
的方程,即
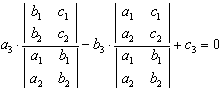 。又因为
。又因为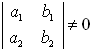 ,所以,
,所以,
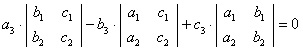 ,即
,即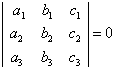 。
。
(充分性)由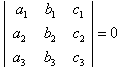 、
、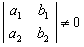 ,得
,得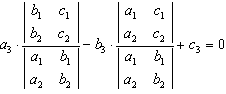 ,即
,即 与
与 的交点坐标满足
的交点坐标满足 的方程,所以
的方程,所以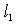 、
、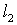 、
、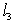 三线共点。
三线共点。
例18 判断下列三条直线是否共点:
(1)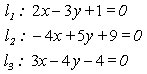 ;(2)
;(2)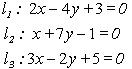 。
。
解 这两组直线显然都是两两相交的。
(1)因为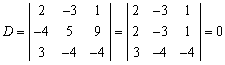 ,所以
,所以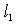 、
、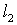 、
、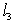 三线共点。
三线共点。
(2)因为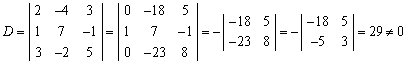 ,所以
,所以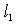 、
、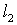 、
、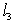 三线不共点。
三线不共点。