
3. 向量积及其应用
已知两个不平行的向量![]() 和
和![]() ,如何求得既垂直于
,如何求得既垂直于![]() ,又垂直于
,又垂直于![]() 的向量
的向量![]() 呢?
呢?
设![]() 的坐标为
的坐标为![]() ,
,![]() 的坐标为
的坐标为![]() ,
,![]() 的坐标为
的坐标为![]() 。因为
。因为![]() 同时垂直于
同时垂直于![]() 和
和![]() ,所以
,所以![]() ,
,![]() ,即
,即
![]() 。(12)
。(12)
将方程组(12)转化为![]() ,由于
,由于![]() 和
和![]() 不平行,所以
不平行,所以![]() ,方程组(12)的解为
,方程组(12)的解为
 。
。
令![]() ,此时
,此时 ,即得
,即得![]() 。
。
![]() 可用基本单位向量表示为
可用基本单位向量表示为![]() ,或记为三阶行列式
,或记为三阶行列式
 。(13)
。(13)
![]() 的模满足
的模满足
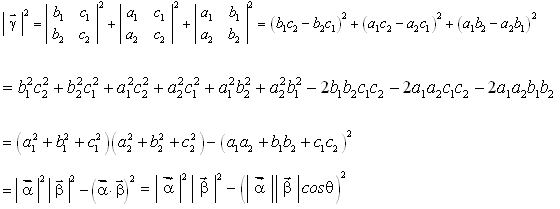
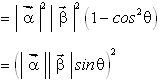
(其中![]() 为
为![]() 、
、![]() 的夹角)。
的夹角)。
即![]() ,它的几何意义是以
,它的几何意义是以![]() 、
、![]() 为邻边的平行四边形的面积(图7-8)。
为邻边的平行四边形的面积(图7-8)。

图7-8
我们把向量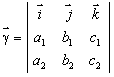 叫做向量
叫做向量![]() 与
与![]() 的向量积,记作
的向量积,记作![]() 。
。![]() 的方向同时垂直于
的方向同时垂直于![]() 、
、![]() (并以
(并以![]() 、
、![]() 、
、![]() 构成右手系),
构成右手系),![]() 的模等于以
的模等于以![]() 、
、![]() 为邻边的平行四边形的面积。向量积的这些特性在立体几何中有广泛的应用,例如求两条异面直线的公垂线方向、求平面的垂线方向、求空间三角形和平行四边形面积、求空间点到直线的距离等。
为邻边的平行四边形的面积。向量积的这些特性在立体几何中有广泛的应用,例如求两条异面直线的公垂线方向、求平面的垂线方向、求空间三角形和平行四边形面积、求空间点到直线的距离等。

