
例19 已知正方体 |
分析 解决这个问题的关键是找到异面直线![]() 和
和![]() 的公垂线段,垂足分别在直线
的公垂线段,垂足分别在直线![]() 、
、![]() 上。因此需要先求出一个与直线
上。因此需要先求出一个与直线![]() 、
、![]() 都垂直的一个向量
都垂直的一个向量![]() ,再找一条端点分别在
,再找一条端点分别在![]() 、
、![]() 上的线段
上的线段![]() ,求得
,求得![]() 在
在![]() 上的投影。
上的投影。
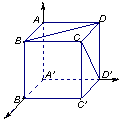
图7-9
解 如图建立坐标系,则得有关点的坐标![]() 、
、![]() 、
、![]() 、
、![]() ,计算得
,计算得![]() 、
、![]() ,于是
,于是![]() 、
、![]() 的公垂线方向是
的公垂线方向是
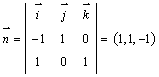 。
。
又因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上的投影
上的投影
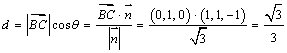 (其中
(其中![]() 为
为![]() 与
与![]() 的夹角)。
的夹角)。
即异面直线![]() 和
和![]() 的距离为
的距离为![]() 。
。
例20 已知空间三点 |
(1)求![]() 的面积;(2)求
的面积;(2)求![]() 的
的![]() 边上的高。
边上的高。
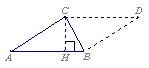
图7-10
解(1)如图7-10,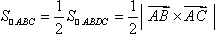 。而
。而
![]() ,
,![]() ,
,
 ,
,![]() 。
。
所以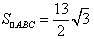 。
。
(2)设![]() 是
是![]() 边上的高,则
边上的高,则
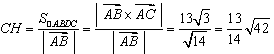 。
。