
自然数的序数理论
经过第一次数学危机,人们对直觉的可靠性产生了怀疑,为使数学建立在可靠的逻辑基础上,建立了数学的公理化方法。自然数是人们最早认识的最基本的数,是在生活和生产实践中依赖于直觉抽象出来的数,人们认识了自然数与实物的“多少”的关系、认识了自然数之间的大小比较、掌握了自然数的某些运算,然而这一切有没有漏洞,是不是合理,有没有矛盾,这些问题在19世纪提上了数学家的议事日程。
德国数学家康托(Georg Cantor,1845-1918年)和意大利数学家皮亚诺(Peano,Giuseppe 1858-1932年)独立地为自然数建立了两种等价的理论--自然数的基数理论和序数理论。这两种理论都用公理化方法定义了自然数的概念,并从自然数概念出发严格论述了自然数的大小关系、运算关系和运算性质等。

康托 皮亚诺
其中基数理论的背景是把自然数与集合的基数建立对应关系,而集合的基数就是该集合中元素的个数。在集合论的逻辑基础上,康托建立了自然数的基数理论。
自然数序数理论的背景是把自然数看作一列有序的元素,这个元素列有无穷个元素,其中有一个是“第一个”,其他的每一个都有唯一确定的前邻元素和后邻元素。在这个基础上建立的自然数公理凸现的是自然数的“有序”特点,因此被称为自然数的序数理论。
在本课程中,我们主要学习自然数的序数理论,经历公理法是如何定义自然数概念,怎样规定自然数的大小,怎样规定自然数的运算,怎样证明自然数的运算性质,体会公理化方法的特征。
定义1 (皮亚诺公理)集合N的元素叫做自然数,如果集合N的元素之间有一个基本关系“后继”(用“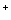 ”表示),并满足下列公理:
”表示),并满足下列公理:
I 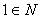 ;
;
II对任何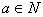 ,有唯一的
,有唯一的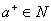 ;
;
III对任何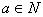 ,
,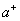 不是1;
不是1;
IV对任何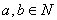 ,若
,若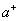 与
与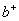 相同,则
相同,则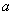 与
与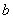 相同,记为
相同,记为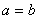 ;
;
V(归纳公理) 若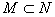 ,且
,且
1) ;
;
2)对任意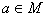 ,有
,有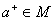 。
。
则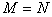 。
。
(说明在这个定义中,“0”不属于自然数,如果按现在的规定,上述定义中的“1”改为“0”就可以了,没有其他本质的差别。在本小节(1.2.2)的叙述中,我们仍然以皮亚诺公理原来的表述为准)
现在我们验证一下,我们早已非常熟悉的自然数是否满足定义l。
由I,集合N中有自然数l;
由III,1是最前面的自然数;
由II,1有唯一的后继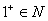 ,记为2,2有唯一的后继
,记为2,2有唯一的后继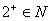 ,记为3,……
,记为3,……
由IV,不同自然数的后继也不同,于是就有了无穷多个不同的自然数:
1,2,3,4,……。
由V,对于自然数N的任意子集M,只要满足“包含1”和“包含各元素的后继”两条,就可知M=N。
(第IV条公理就是数学归纳法的依据)
定义2 (自然数的加法) |
在自然数N中,满足下列条件的二元运算“+”叫做加法:对于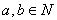 ,满足
,满足
1)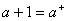 ;
;
2)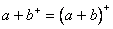 。
。
其中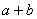 叫做
叫做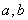 的和。
的和。
按加法的定义,加法应该如何做呢?
定理1 自然数的和存在且唯一。
证明设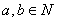 ,取定
,取定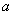 ,
,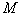 是使
是使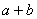 唯一存在的自然数
唯一存在的自然数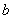 的集合,
的集合,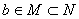 。
。
1)当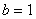 时,
时,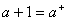 ,由公理第II条,
,由公理第II条,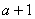 在自然数中存在且唯一。
在自然数中存在且唯一。
2)假设当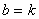 时,
时,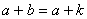 在自然数中存在且唯一。那么
在自然数中存在且唯一。那么
当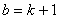 时,
时,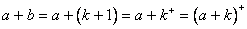 (理由:后继定义,加法定义),
(理由:后继定义,加法定义),
由于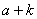 在自然数中存在且唯一,由公理第II条,
在自然数中存在且唯一,由公理第II条, 在自然数中存在且唯一。
在自然数中存在且唯一。
由公理第V条知,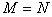 。
。
所以,对任意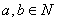 ,
,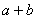 在自然数中存在且唯一。
在自然数中存在且唯一。
定理2(加法结合律)对任何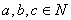 ,总有
,总有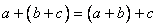 。
。
证明取定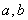 ,设
,设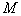 是使
是使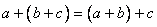 成立的自然数
成立的自然数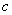 的集合,
的集合,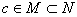 。
。
1)当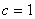 时,由于
时,由于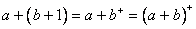 ,而
,而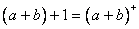 ,因此
,因此
 。
。
2)假设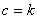 时,有
时,有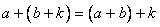 。
。
当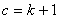 时,
时,
因为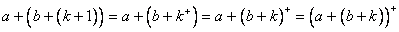 ,
,
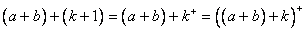 ,
,
由假设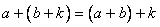 和公理第II条,得
和公理第II条,得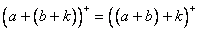 。即
。即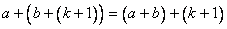 。
。
由公理第V条得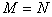 ,即对任意
,即对任意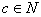 ,满足
,满足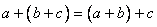 。
。
定理3 (加法交换律)对任何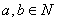 ,总有
,总有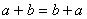 。
。
证明取定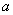 ,设
,设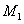 是使
是使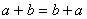 成立的自然数
成立的自然数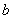 的集合,
的集合,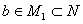 。
。
1)当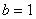 时,为了证明由于
时,为了证明由于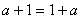 ,设
,设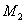 是使
是使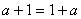 成立的自然数
成立的自然数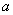 的集合,
的集合,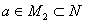 。
。
i)当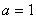 时,显然
时,显然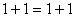 成立。
成立。
ii)假设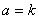 时,有
时,有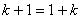 ,
,
当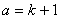 时,
时,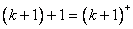 ,
,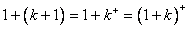 ,
,
由公理第V条得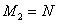 ,即对任意
,即对任意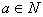 ,满足
,满足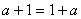 。
。
2)假设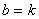 时,有
时,有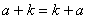 ,
,
当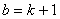 时,
时,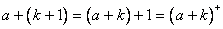 ,
,
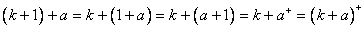 ,
,
又由于假设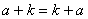 和公理第II条,得
和公理第II条,得
 。
。
由公理第V条得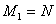 ,即对任意
,即对任意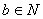 ,满足
,满足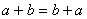 。
。
(注1)加法交换律的证明用了两次公理第V条:首先对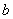 进行归纳,当
进行归纳,当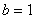 时,要证明
时,要证明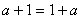 ,此时又对
,此时又对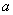 进行归纳。
进行归纳。
2)在证明 成立时,用了
成立时,用了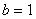 时的结论和
时的结论和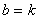 时的假设,还用了定理2(加法结合律))
时的假设,还用了定理2(加法结合律))
(定理1、定理2、定理3的证明可以不讲)
定义3(自然数的乘法) |
在自然数N中,满足下列条件的二元运算“·”叫做乘法:对于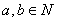 ,满足
,满足
1)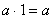 ;
;
2)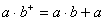 。
。
其中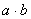 叫做
叫做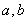 的积,简记为
的积,简记为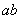 。
。
定理4 自然数的积存在且唯一。
(严格的证明要用到公理V,本节省略这部分证明)
定义了自然数的乘法运算以后,我们也要证明乘法的运算律:
定理5(乘法分配律)对任何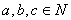 ,有
,有
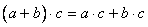 ,
,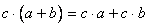 。
。
定理6(乘法交换律)对任何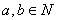 ,有
,有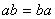 。
。
定理7(乘法结合律)对任何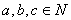 ,有
,有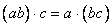 。
。
现行在中小学教材上这样表述“关于乘法,3个5,可以写作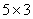 ,也可以写成
,也可以写成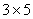 …。3和5都是乘数”。这里不强调
…。3和5都是乘数”。这里不强调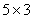 和
和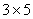 的区别,也不强调乘数与被乘数的区别,原意是为了减少学生学习乘法运算的困难,但事实上,
的区别,也不强调乘数与被乘数的区别,原意是为了减少学生学习乘法运算的困难,但事实上,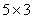 具有乘法定义的背景,而
具有乘法定义的背景,而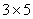 是在乘法定义的基础上,又运用了乘法的交换律。
是在乘法定义的基础上,又运用了乘法的交换律。
自然数的序数公理中,已经用“后继”,规定了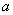 与
与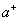 的顺序,现在我们讨论任意两个自然数的顺序。
的顺序,现在我们讨论任意两个自然数的顺序。
定义4(半序集)如果在集合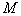 上定义了一种关系“
上定义了一种关系“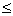 ”,若对于任意的
”,若对于任意的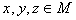 ,满足条件
,满足条件
1)(自反性)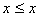 ;
;
2)(反对称性)如果有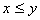 ,且
,且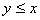 ,那么
,那么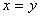 ;
;
3)(传递性)如果有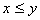 ,且
,且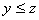 ,那么
,那么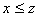 。
。
则称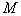 为半序集或偏序集,“
为半序集或偏序集,“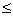 ”称为半序关系。
”称为半序关系。
若半序集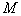 进一步满足
进一步满足
4)对于任意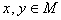 ,
,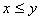 和
和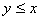 两式中至少有一个成立,则称
两式中至少有一个成立,则称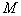 全序集。
全序集。
若全序集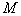 满足
满足
5)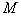 的任意非空子集
的任意非空子集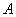 ,都有最小元
,都有最小元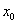 ,即任意
,即任意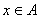 ,有
,有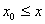 ,那么
,那么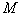 称为良序集。
称为良序集。
我们可以验证,自然数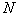 是关于“
是关于“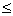 ”关系的良序集。
”关系的良序集。
自然数有两种属性,一是基数属性,一是序数属性。自然数的基数理论体现了一个集合有“多少个元素”的属性,自然数的序数理论体现了数的顺序性,即“第几个元素”的属性。这二者是相通的,共同反映了事物具有的数的特性。我们以自然数的序数理论定义了自然数,定义了自然数的加法和乘法,并可以用严格的逻辑演绎的方法证明自然数的一系列运算法则,这一切与“自然”发生的自然数概念和运算完全是相容的。本节的学习目的是让学习者了解现代数学中公理化的方法和过程,体会到公理化方法的严谨性、抽象性和可靠性。