
数学归纳法 |
由自然数序数公理的第V条(归纳公理),很容易得到下列定理。
定理8(数学归纳法)设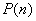 是关于自然数
是关于自然数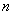 的命题,若
的命题,若
1)(奠基)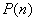 在
在![]() 时成立;
时成立;
2)(归纳) 若在![]() (
(![]() )成立的假定下可以推出
)成立的假定下可以推出![]() 成立,
成立,
则![]() 对一切自然数
对一切自然数![]() 都成立。
都成立。
定理8 给出的方法叫做第一数学归纳法,它是数学归纳法的标准形式。
适当改动定理8中奠基部分,可得到第一数学归纳法的一些变形形式。
推论1 设![]() 是关于自然数
是关于自然数![]() 的命题,若
的命题,若
1)![]() 在
在![]() 时成立;
时成立;
2)(归纳)若在![]() (
(![]() )成立的假定下可以推出
)成立的假定下可以推出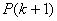 成立,则
成立,则![]() 对一切自然数
对一切自然数![]() 都成立。
都成立。
推论2 设![]() 是关于自然数
是关于自然数![]() 的命题,若
的命题,若
1)![]() 在
在![]() 时成立;
时成立;
2)(归纳)若在![]() (
(![]() )成立的假定下可以推出
)成立的假定下可以推出![]() 成立,则
成立,则![]() 对一切自然数
对一切自然数![]() 都成立。
都成立。